TITLE: Taxonomy for INM-Neuron

AUTHOR: Gerd Döben-Henisch

First Version: 16.11.98 10:55

Last Version: 16.11.98 19:58

SUMMARY: There is a vast literature about mathematical properties of different types of neural nets. Using results of Wolfgang Maass (TU Graz) we can show that the INM-Neuron is a 3rd Generation Neural Net which is based on socalled ‚spiking neurons'.

References:

MAASS, Wolfgang, [1997], Networks of Spiking Neurons: The Third Generation of Neural Network Models, MS, Institute for Theoretical Computer Science, TU Graz [NSN]

DUDEL, J./ MENZEL, R./ SCHMIDT, R.F. (eds), [1996] Neurowissenschaft. Vom Molekül zur Kognition, Springer

PENZLIN, Heinz [1996, 6th ed.], Lehrbuch der Tierphysiologie, Gustav Fischer Verlag, Jena-Stuttgart.

SHEPHERD, Gordon M. [1994, 3rd ed] Neurobiology, Oxford University Press, New York -

Oxford

SHEPHERD, Gordon M. (ed) [1998, 4th ed] The Synaptic Organization of the Brain, Oxford

University Press, New York - Oxford

During the summer 1998 we developed at the INM a formal model of a neuron based on the data available in the standard textbooks in the field of Neurobiology. We called this model INM-Neuron. Very soon we had also a prototype implemented in a computerprogram (Prolog) which we showed publicly at the CebitHome Faire (Hannover, Germany, Aug. 98).

What was missing so far was an evaluation of the mathematical properties of this INM-Neuron compared to the already existing mathematical models around.

This deficiency could now be remedied on account of the work of Wolfgang Maas of the TU Graz (Austria). He has in several papers and books analyzed what he calls ‚spiking neurons'. It turns out that the INM-Neuron can be identified as an instance of the general class of spiking neurons.

To make this explicit I will review shortly the main message of an article (Maass 1997) written by Maass and then I will explain how the INM-Neuron relates to this.

Wolfgang Maass distinguishes three types of neuron models:

• First Generation Neurons: McCulloch-Pitts neurons/ Perceptrons/ ‚threshold gates' . From these emerged multilayered perceptrons, Hopfield nets, and Boltzmann machines. They can compute any boolean function as well as all digital functions.
• Second Generation Neurons: applying activation functions with a continuous set of possible output values to a weighted sum of the inputs (e.g. sigmoid functions, linear saturated functions, piecewise exponential functions). From this emerged feedforward and recurrent sigmoidal neural nets and networks of radial basics function units. These networks can also compute any boolean function, besides digital functions they can also approximate sufficiently accurate any continuous function with a compact domain/ range; they support learning algorithms based on gradient descent.
• Third Generation Neurons: ‚spiking neurons' (‚integrate and fire neurons'). In networks of spiking neurons plays the timing of individual computation steps a key-role for the computation.

To understand how the INM-Neuron relates to this taxonomy one has to take a short look to the definition of ‚spiking neurons'.

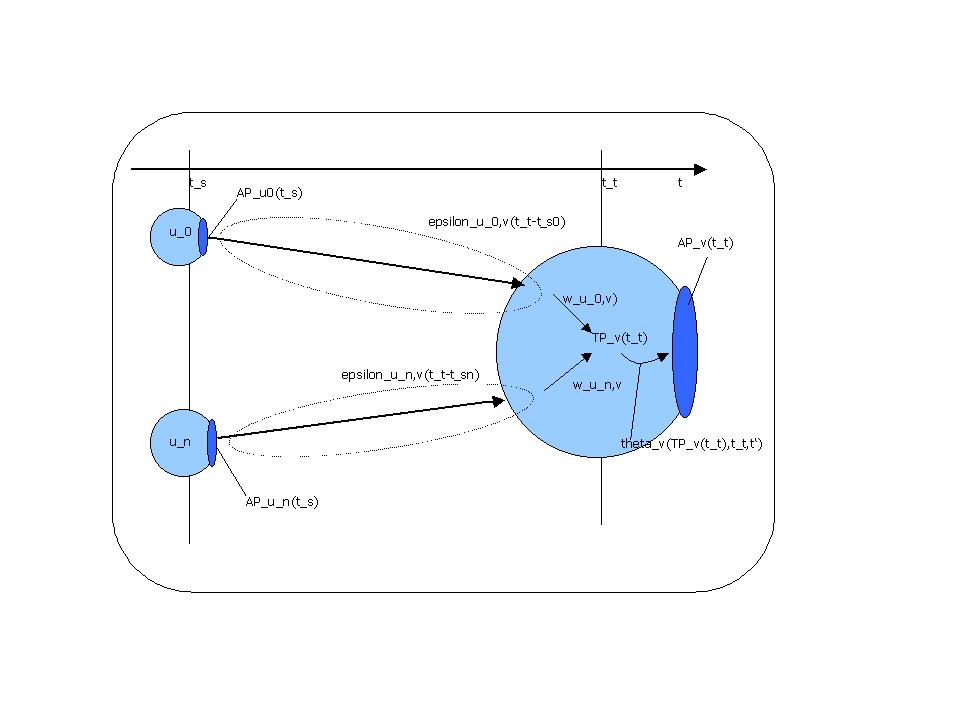
The following definition of a Spiking Neuron Network [SNN] is a slightly modified version of that given by Maass (1997).

V := Set of spiking neurons

W := Set of weights (W c Real+)

F := Set of firing timepoints (F c Real+)

P := Set of potentials (P c Real)

E := Set of connections (synapse-membran or gap junction) (E c V x V)

epsilon := Response function, epsilon c E x T x T --> P; epsilon_u,v(t_t,t_s); Response function for the connection between the input neuron v firing at time t_s and the neuron u receiving input at time t_t.

theta := Threshold function, theta c V x P x T x T --> P; theta_v(p,t_t,t'). Threshold function at time t_t for the neuron v receiving several weighted inputs as triggering potential p with a last action potential at t'.). If neuron v has fired at time t' it will not fire before t'+c1 (:= ‚absolut refractory period'); between (t+c1, t+c1+c2) (:= ‚relative refractory period') the ‚triggering potential' P_v(t_t) deviates from ‚normal'.

Axioms_snn(1)(Triggering Potential): TP_v(t_t) = SUM(<u_i,v> in E) SUM(t_s in F; t_s < t_t, t_s > t') W_u_i,v * epsilon_u_i,v(t_t,t_s)

/* The triggering potential TP results from the sum of all weighted response functions. It is restricted to the timewindow between (t',t_t). */

Axiom_snn(2)(Activation Potential): AP_v(t_t) = theta_v(TP_v(t_t),t_t,t').

/* The activation potential AP results from the triggering potential ‚filtered' by the threshold function theta. */

Axiom_snn(3)(Base Threshold): If t_t-t' > c3 then theta_v(TP_v(t_t),t_t,t') = theta_v(TP_v(t_t),0)

/* If the following triggering potential occurs beyond the refractory period the behavior of the neuron is similar to the case where the action potential has no preceding history.*/

DF (Linear Temporal Coding): If x is a numerical input variable x in Real then x' = T_input – x * c and c > 0. If y is a numerical output variable y in Real then y' = T_output – y * c and c > 0.

Assuming networks of spiking neurons with regard to temporal coding with single spikes, MAASS proofs that this computational model has at least the same computational power as neural nets from the first two generations (i.e. multilayer perceptrons and sigmoidal neural nets) of a similar size. Furthermore he can exhibit concrete functions which require for their computation significantly fewer neurons in a network of spiking neurons (cf. NSN 21).

The INM-Neuron fits well in the definition of a spiking neuron given above. Therefore all of the results reported by MAASS are also valid of networks with the INM-Neuron.

What distinguishes the INM-Neuron from the above given definition of a spiking neuron is the fact that within the INM-Neuron Model the response function and the threshold functions are given as concrete functions simulating a chemical machinery which ‚behaves' like these functions, i.e. if you have in the spiking neuron model the abstract epsilon function, you have in the INM Neuron model the concrete machinery of an axon with compartements followed by a complex synapse with possibly several membranes and finally a postsynaptic membran; all these parts together are forming the epsilon function in the INM-Neuron. The same holds for the action potential/ threshold function; both are realized in the INM-Neuron Model as a complex membran model which can be triggered by a triggering potential and which reacts according to it's actual state of receptors, ionic channels, ionic pumps and substance concentrations.

The following table gives a short summary of the similarity and differences of the general ‚spiking neuron' and the more specific INM-Neuron: