Knowbotic Interface Project
Software Engineering Context
This
is a working paper which will probably be rewritten several times in the next months
AUTHOR: Dr. Gerd Döben-Henisch
COLLABORATORS: Leo Pos und Thore Swindall
FIRST DATE: December 27, 1995
DATE of LAST CHANGE: March-25, 1996
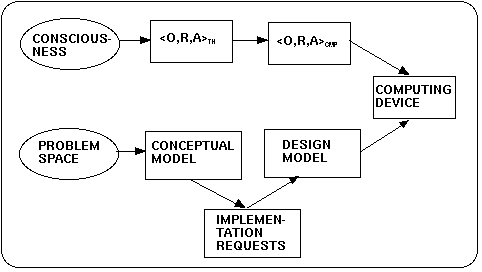
The context of the discussion of the relationship between the KIP II theory and a
computer simulation is given by the following four factors (cf. figure below): (i) we assume a consciousness (see Introduction) which produces (ii) formal theories which are characterized by objects, relationships, and axioms (see Theory). Theories are a kind of articulation of analyzable structures of the consciousness (see Phenomenological Struktur). We assume further (iii) computational representations of the formal theories which can (iv) be implemented in a computing device as working programs.
This context has strong relationships with the task of Software Engineering as it is understood within the object oriented paradigm (cf. (DILLON 1993:3f, 24ff), (MARTIN 1995:337f), (ELLIS 1994:237ff), (RUMBAUGH 1993)): The problem space is given as a set of concepts shared by the members of a team. In a first approach one constructs with all participants a problem description (PD) in natural language. This description represents the problem space in a communicable form and serves as the common platform for the construction of an explicit and conceptually complete conceptual model. Befor the final realization of the model one has then to examine possible implementation requests. The modifications of the conceptual model with the implementation requests leads to the design model. The design model provides the definitiv framework for the implementation of the final source code on some real computing device (cf. figure below).
In KIP II we will follow a pragmatical strategy related to the development of a formal theory and a software model: with respect to a formulated problem space we will construct an object oriented conceptual model in parallel with a formal structural theory. The connection between the formal theory and the computer model will therefor only exists through a mapping between the graphical representation of the conceptual model and the formal description of the theory (cf. figure below). Later on (probably in KIP III) we have to reexamine this problem trying to set up a more formal description of this relationship.
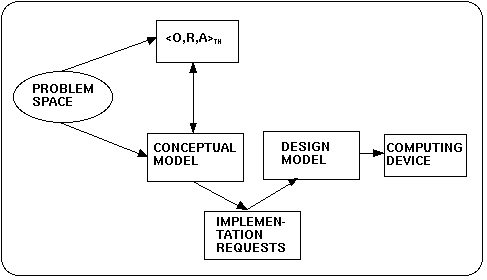
We decided to proceed in this 'pragmatic' way because there are too many theoretical questions unsolved with regard to the relationship of our theoretical theory and and the computer model.
Ideally it should be possible (i) to translate a formal structural theory automatically 1-to-1 in a software model and there should also exist (ii) an automatic procedure to translate the software model 1-to-1 into a source code. If the means used for the construction of a software model do all belong to the area of computational structures then the claim (ii) can principially be fullfilled. Claim (i) can not be fullfilled if one uses conceptual means which are 'richer' than the computational demands allow. This is the case if one e.g. uses a full version of predicate logic or a set theoretical language. In the case of KIP II it is an open question how 'rich' the used descriptive means have to be. We will start with an unrestricted set theoretical language. This implies that there will be a real gap between our conceptual model and the software model. This is due to the famous results of Gödel (GÖDEL 1931) and Turing (TURING 1936).
Continue with Constructing a conceptual model.
Comments are welcomed to kip-ml@inm.de
Daimlerstrasse 32, 60314 Frankfurt am Main, Deutschland. Tel +49- (0)69-941963-0,
Tel-Gerd: +49(0)69-941963-10